 A chord inversion is when another note in a chord in played in the bass. If a chord has 3 notes (triad) there are 2 possible inversions – the 3rd in the bass is called the first inversion and the 5th in the bass is called the second inversion. If a chord has 4 notes (4 part harmony) there are 3 possible inversions – the first and second inversions are the 3rd and 5th in the bass respectively (just like the triads) and the third inversion is the 7th in the bass When I teach inversions I have my students practice every permutation of inversions in their progressions. This can create interesting bass movement and add a lot to your playing. In the next blog I'll explore several specific ways of doing this. Another way to utilize inversions is: when you're playing a chord for say two measures, a measure or two beats you could play, respectively, a measure on a chord and a measure on one of it's inversions, two beats on a chord and two beats on one of it's inversions or one beat on a chord and one beat on one of it's inversions. Lastly, you should also practice cycling through inversions, for ex) play a Cmaj7 for two beats then it's first inversion (Cmaj7/E) for two beats then it's second inversion (Cmaj7/G) for two beats and finally it's third inversion (Cmaj7/B) for two beats and do this process for every chord. 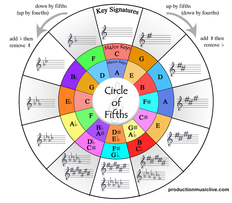 Now that you know how to calculate the number of accidentals in each key, the next step is to learn which notes are sharp of flat). There's a concept called the “order of flats” and it's inversion, the “order of sharps”, there are the specific sequence of flats and sharps the occur in the keys (the right hemisphere uses sharps and the left uses flats). To calculate the order of flats, simply start at 5 o'clock and proceed counter-clockwise through 11 o'clock = B – E -A – D – G – C – F and conversely and conveniently, the order of sharps is the reverse of the order of flats: 11 o'clock proceeding clockwise through 5 o'clock = F – C -G -D -A -E – B. Thus far, we've only be discussing major keys, there are also 12 minor keys encapsulated in the circle of fifths (these minor keys are relative to the major keys) To calculate them begin with Am at 12 o'clock and proceed clockwise in 5ths =Am – Em – Bm – F#m – C#m – G#m. Then proceed counter-clockwise in 4ths = Am – Dm – Gm – Cm – Fm – Bflatm – Eflatm. |
AuthorEric Hankinson Archives
December 2023
Categories
All
|
|
The Chromatic Watch Company
(my other business) |
|

 RSS Feed
RSS Feed

